耐驰首席技术官徐梁：级数反应与自催化反应

  在热分析领域积累了十余年丰富的理论与实践经验，是行业内资深的热分析应用专家。谈及热分析动力学，徐梁重点介绍了热分析动力学中的级数反应与自催化反应，并以环氧树脂的热固化为例，讲解了怎么样做机理函数的判断与选择。

  一、热分析动力学概述化学动力学是近代物理化学的一门重要分支，它对实践中千变万化的各类化学反应，从反应速率和反应机理角度进行抽象研究，涉及的重要变量有时间、温度、浓度、压强、催化剂、溶剂等。

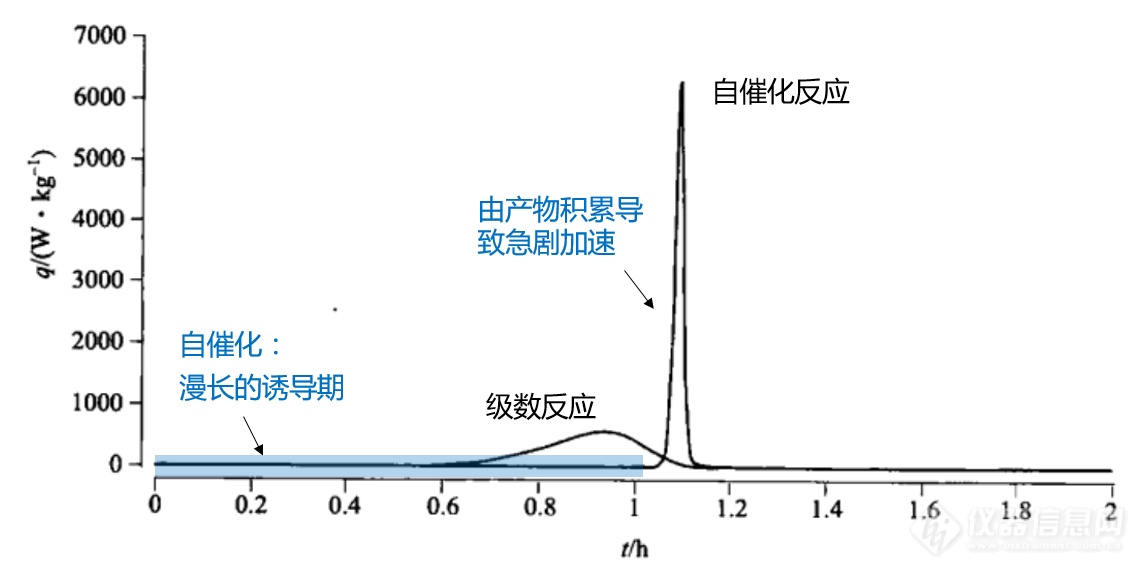
  热分析动力学是对化学动力学的一种简化，它与DSC、TGA为代表的热分析技术结合紧密，将热分析测试手段中不常涉及、或很难研究的一些因子作了简化或合并，从而将反应速率仅仅表示为时间、温度与转化率三个变量的函数。其基本方程的微分形式为：

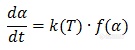
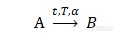
  在这里，t为时间，T为温度，α为归一化转化率。dα/dt(后文有时简写成

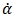
  )则为转化率随时间的变化率，在经典热分析动力学的范畴内，它仅取决于以下两项：

  k(T)：速率常数项，表征反应速率与温度的相关性。通常用阿伦尼乌斯方程的形式：

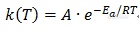
  其中Ea是表观活化能，常用单位kJ/mol。从物理化学角度这一项与反应的激活能位垒有关，在现象层面则与反应速率随温度而变的特性直接相关。活化能越高，改变反应温度对速率的影响越大。A则为指前因子，又称频率因子，是一个直接的正比系数。R为气体常数，R=8.314 J/(mol*K)。

  α)：机理函数项。表征反应速率与转化率的相关性，可视为对反应机理的数学描述。这一项最为灵活多变，有形形的机理函数用来描述不同的反应机理，常见的有级数反应、自催化反应、相边界反应、成核生长反应、扩散障碍反应等大的类别，每一类别包含多个不同的机理函数，用于细化对不同反应的描述。至于化学动力学中的其他变量，或被略去(如绝大多数热分析测试在常压下进行，因此压强因子被略去)，或被归一化处理(如浓度的相对变化被归一化处理为转化率，见后文)，或被简并到正比项A(例如分子摩尔浓度、体系粘度、分子截面积等其它影响分子碰撞几率的因素)、指数项Ea(由此Ea被称为“表观活化能”而与真正物化意义上的激活能有一定差别)、甚至机理函数(例如反应界面的几何特性)之中。

  由上分析可见，热分析动力学本质上是一种唯象科学，它仅用于对千变万化的热分析数据来进行数学层面的抽象与处理，例如对于常见的TGA测试数据，由于失重比例(100%→x%)可归一化为转化率α（0-1），因此一条TGA曲线本质上就是（

  (类似于DTG)。DSC曲线与此相似，经一定的修正预处理后，峰面积比例可处理成转化率，对其求导可得到转化速率(形状上类似于DSC热流信号)：

  )关系曲线，然后被套入基本方程中进行求解。在求解方式上有无模型动力学与模型动力学两大体系，不管使用哪一种方法，最终都是要求得方程中的Ea、A、以及f(α)相关参数等项，即获取完整的、仅包含（)随时间(t)、温度(T)、以及温度微商(升降温速率dT/dt，一般写成β)的演变规律可视为已知。因此从方程出发，可对实际不同控温程序下的反应进程进行预测，或按照速率控制要求对控温程序进行模拟优化，用以指导实际控温工艺，获取期望的反应进程。

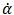
  以上是对热分析动力学作一全景式的概略介绍。热分析动力学作为物理化学与实验技术相结合的一门分支学科，所涉甚广。篇幅所限，下文仅对均相反应体系中常用的两大类机理函数：级数反应与自催化反应作进一步的讨论。

  所谓均相反应体系，指的是反应物分子均匀地分布在反应体系中，宏观上各区域之间无显著的浓度差，在任一时刻体系各处的反应速率相同的一种理想状态。在这种反应体系中，除温度之外，分子浓度及其变化是决定反应速率的主导因素。

  与之形成对比的是，异相(也称为非均相)反应体系有着明显的反应界面的概念，分子的化学反应仅发生在一定的反应界面上。在这种体系中，浓度的变化不再是速率的主导因素，事实上，在界面之外，分子从始至终保持原始浓度，而反应速率为零。除温度之外，决定界面上的反应速率的，仅只是反应界面的几何特性，及其随时间的演变方式(扩展，收缩，增厚)、演变维度(一维、二维、三维)。

  不管是均相还是异相体系，都只是一种理想化的数学模型。实际的化学反应体系往往更复杂，但在小尺度反应(例如热分析的小量样品测试)、传质传热理想化的情况下，大体可归为这两类体系之一。在热分析领域，均一的纯液相反应(例如溶液中的反应)一般可归为均相反应，涉及多相的反应(气固、液固、气液、固固多相、液液多相)一般为异相反应，个别反应界面概念模糊的纯固相反应有时也可简化处理为均相反应。在获取了小尺度反应模型之后，对于实际工业应用的尺度放大，应附加传质传热的相关修正。

  必须要格外注意的是，这里的均相、异相涉及的是反应物与产物的相态，而与材料本身是否成分均匀、单一无关。例如固体的结晶反应，虽然材料的化学成分很纯，但由于晶区与非晶区相态不同，反应为异相反应。而纤维增强预浸布中的液态树脂的固化反应，尽管宏观材料为复合材料，包含多种成分(树脂，纤维等等)，甚至在小尺度上纤维增强体的分布都不一定均匀，但假如不考虑树脂与纤维之间的相互作用，把固化反应简化为主要在液态树脂内部进行，仍然可视为均相反应。

  级数反应是最简单、也是最常用的一种均相反应模型。这里考虑的是反应过程中，反应物的浓度下降对反应速率的影响。其通式为：

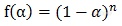
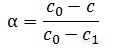
  例如体系中反应物的初始浓度为0.7mol/L，反应结束时反应物浓度下降为0.2mol/L(实际反应中反应物不一定消耗完全)。则该浓度的相对变化被归一化处理为0-1的转化率。即：

  这里1-α与反应物在反应过程中的相对剩余量相对应，而我们似乎丢失了绝对摩尔浓度的相关信息。事实上，反应物浓度为0.7mol/L、还是7mol/L，对反应速率当然有影响，但该影响已被抽离、并归到正比因子A之中。摩尔浓度高的体系，分子碰撞几率大、或者说碰撞频率较高，反应速率通常较快，因此频率因子A会较大。由此使用经典的热分析动力学方法，对同一反应、不同摩尔浓度下的测试结果进行建模，指前因子很可能不同。这是需要注意的一点。

  在均相体系中，级数为整数、具有明确物理化学意义的级数反应，常见的有如下两种：

  ：n=1，f(α)=1-α。即在温度不变的情况下，反应速率与反应物的相对剩余量成正比，或者说在反应过程中，随着反应物的消耗与转化，反应速率同比下降。这种情况常见于均相体系中的单分子反应 A à B，例如分子内结构重排、自发衰变、部分液相分解反应等。

  ：n=2，f(α)=(1-α)2。在温度不变的情况下，反应速率与表观反应物相对剩余量的平方成正比，常见于液相中的双分子反应，例如 2A→B。我们再从数学上观察一下，对于

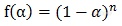
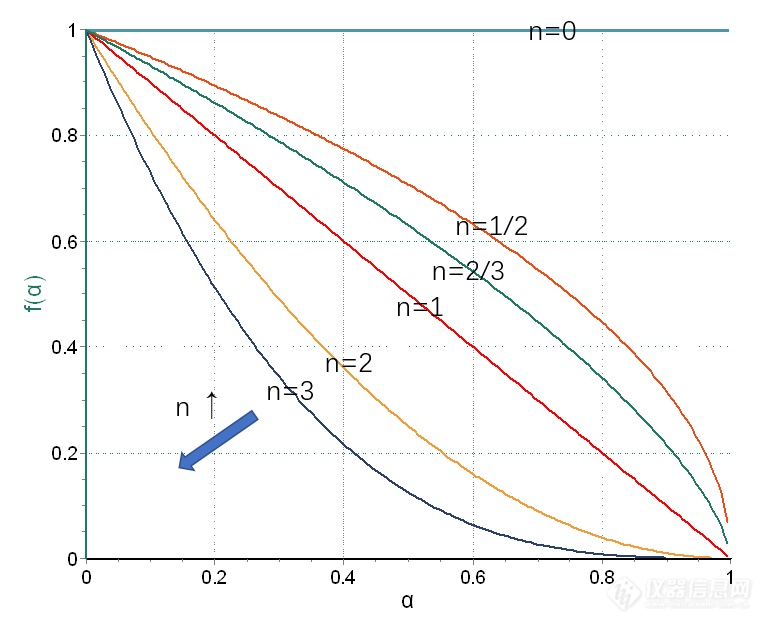
  1. 所有曲线的最大值均出现在起点处。这在某种程度上预示着在温度不变的情况下，级数反应以开始发生时速率最大，随后速率单调下降。

  2. 以n=1为对角线，n越大，f(α)随α衰减越快，表明反应级数越高，随着反应物的转化，反应速率下降趋势越明显。

  从物理化学角度，反应级数应为正整数，且很少超过3(多于三分子共同参与的合成反应很少见)。但从表观动力学的数学拟合意义上，反应级数可以是非整数，取值范围可以超过3，也可以小于1，但这样的一种情况往往是内在非均相反应机理的表现。例如用级数函数拟合，级数超过3或更高，表明反应速率随着反应物的转化而迅速下降，有可能涉及到产物堆积于界面的界面扩散障碍反应;若级数小于1，有可能牵涉到界面收缩的相边界反应，例如n=2/3对应界面球状收缩的三维相边界反应，n=1/2对应界面柱状收缩的二维相边界反应，n=0(零级反应)对应界面面积不变的一维相边界反应。

  自催化反应，有时也称为自加速反应，是指随着反应的进行，产物的生成会对反应起到促进作用。这类反应的机理函数通式为扩展的Prout-Tompkins方程(Bna)：

  这里1-α对应于反应物的相对剩余量，α对应于产物的相对生成量，而反应速率同时是这两者的函数，随反应物的消耗而速率下降，随产物的生成而速率上升。从物理化学角度，这类反应常见于发酵反应、聚合反应、链式反应等。

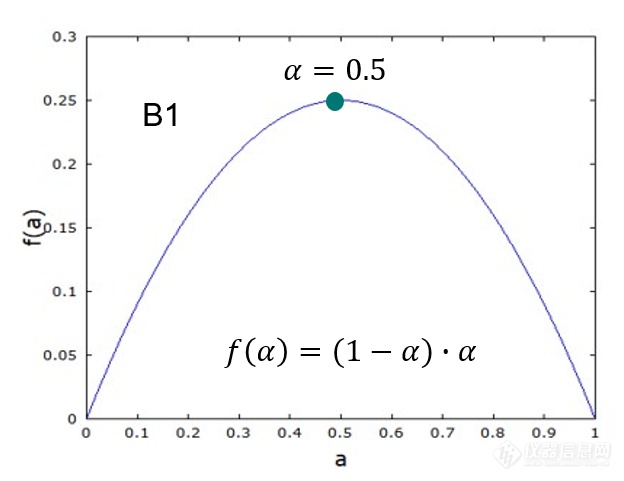
  最简单的自催化反应是Prout-Tompkins方程(B1)，即上式中的n、m两个级数均为1：

  在这里，反应速率本应随着A的消耗而下降，但产物B一旦生成，即作为反应物之一，参与并促进了反应的进行。因此在反应的起始阶段，当B的量甚小时，反应速率不高;在反应的终止阶段，A的剩余量已降至甚低，反应速率也不高。反应最大速率点将出现在A与B的量均较充分的阶段，即反应的中期阶段。这一点可通过对B1方程的作图得到验证：

  级数反应与自催化反应的差异，在等温实验下表现最明显。在理想的等温条件下，温度因子k(T)项为常数，动力学方程可简化为：

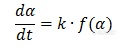
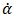
  直接成正比。而从之前的讨论可知，对于级数反应，f(α)随转化率α单调下降;对于自催化反应，f(α)的极值约出现在反应的中期阶段。实际的等温测试得到的是 (DSC、DTG)随时间t的演变关系，涉及到对上式进行积分，得到α(t)函数后再对t求导，稍微复杂一些，这里不作具体的数学推导。但不管怎样，由于α与t是同向变化关系，因此以上的规律依然存在。结合物化意义来讲，等温条件下，对于级数反应，反应速率与反应物的量相关，在起始反应时反应物浓度最高，此时反应速率最大，随后跟着时间的演变、反应物的消耗而逐渐减速;而对于自催化反应，在反应早期，由于产物B的量很少，对反应的催化作用很不明显，因而此时反应速率甚低，而由于反应速率低，B的量积累很慢，体现在反应初期阶段漫长的低速“诱导期”。当B的量积累到某些特定的程度时，对反应的催化加速效应逐渐明显，随着反应速率的加快又促成了B的大量生成，进一步加速反应，因此在反应中期，反应会有一个快速的提速期。到反应后期，随着反应物A的严重消耗，反应速率再度下降，直至反应完成。

  这里除了f(α)变化对速率的影响外，还混入了温度的连续上升对反应的加速作用。因此即使是级数反应，最大速率点也不再出现在反应起始处。事实上，以一级反应为例：

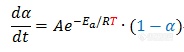
  )，f(α)项的下降倍率不超过50%，而由温度T上升导致的指数式增速效应要显著得多。因此反应前期速率将逐渐增大。到反应后半程，f(α)将以越来越小的数字乘入到整个速率方程中，即f(α)倍率式减速效应占据主导，因此反应后期速率将逐渐减小。对于自催化反应，反应初期f(α)甚小，同时温度也较低，因此反应早期阶段整个反应速率都很低，呈现漫长的诱导期，直至随着产物的积累、f(α)的变大，加上温度上升的增速效应，反应可能出现较突然的加速。随后随着反应的快速转化、f(α)的快速减小而减速。

  因此在动态升温图谱上，这两种类型反应均体现为“峰”，而自催化反应往往“基线”更平、峰形更尖窄。

  单纯的自催化函数，在实际应用中用得较少。道理很简单，若将Prout-Tompkins方程代入动力学方程：

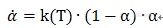
  在反应起始点，转化率α=0，此时反应速率 。而反应速率为零，意味着反应不会发生，α将始终为0!

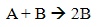
  反应的进行必须有B的参与。除非在反应体系的初始状态下直接混入一定量的B，否则若以纯A作为起点，在没有B的参与下永远都不可能有第一个产物B生成，也就从另一方面代表着反应永远都不可能发生。

  即A本身能独立转化为B(或许速率较慢，但有一定的转化几率)，而A也可在B的“催化”下生成B(通常更有效)。

  这类反应可称之为复合式自催化反应，在假设两个路径活化能相同的情况下，机理函数通式为Cnm：

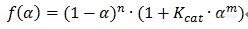
  仔细观察上式可知，这一方程是Fn与Bna两项的加和，在Bna项前加了权重因子(自催化系数)Kcat。

  该方程的简化函数有C1(级数项n、m均等于1，即F1与B1的组合)、Cn(m=0，反应物以级数n、而产物以一级形式参与自催化)。其中Cn较为常用。

  另如果考虑两个路径活化能不同，有Kamal-Sourour型动力学方程：

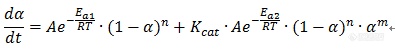
  作为级数反应与自催化反应的混合，复合式自催化反应在加速特性方面将介于纯级数反应与纯自催化反应之间，即存在一定的诱导期，在诱导期之后，其反应加速相比级数反应显得较为显著，但又不如纯自催化反应那么突然。当然具体加速表现还取决于两个路径之间的组合权重。

  前文已详细讨论了对于均相反应体系，不同的反应类型(级数反应、自催化反应、复合式自催化反应)，其反应进程的特性表现。这里我们将通过对某一环氧树脂固化反应的DSC曲线的动力学拟合，来帮大家更直观地理解三者的差异。

  下图在三个不同的升温速率(5、10、20K/min)下进行了DSC测试，得到了环氧树脂的固化放热峰。

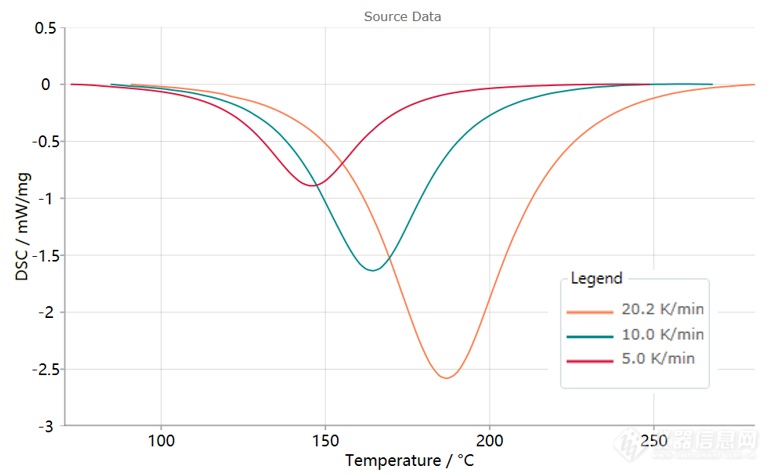
  有相关论文表明环氧树脂的固化为自催化反应。但这里我们先将该论断放在一边，假设我们完全不了解该反应的内在化学机制，因此尝试用不同的机理函数进行拟合，通过拟合匹配的优劣来判断可能的反应类型。

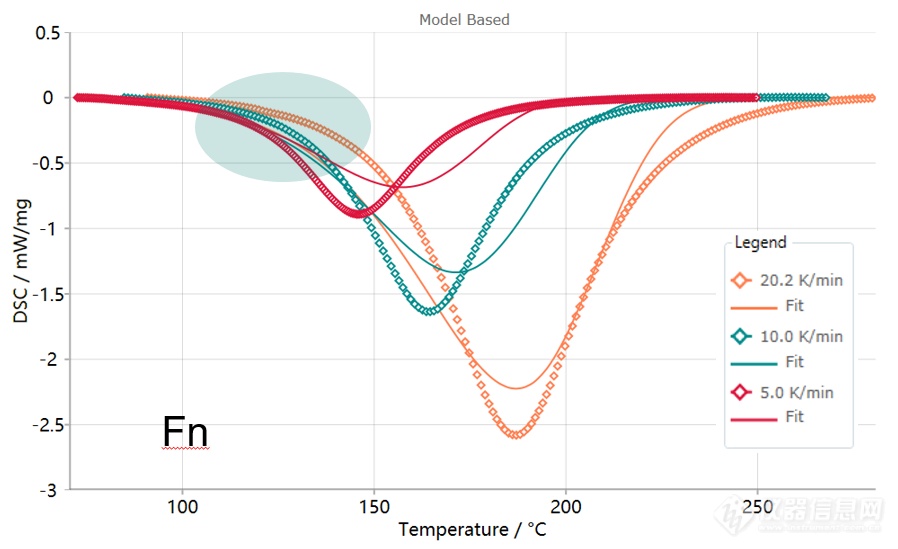
  下图彩点为实测曲线，实线为使用级数反应Fn对实测曲线的拟合。我们先前已知DSC信号直接对应于反应速率。

  将拟合线与实测线相对比，着重关注反应前期阶段，可见级数反应无显著的诱导期，加速较为温和，而实测信号左侧水平区较为显著，随后的加速也较为显著(实测线的峰左侧较拟合线更为陡峭)，表明反应可能牵涉到自催化机制。

  下图尝试用纯自催化函数Bna进行拟合。总体拟合质量得到了很大改善，但反应早期阶段仍拟合不佳。从拟合实线可见，纯自催化反应的诱导阶段更长、更接近水平，而随后的加速阶段上升更快。

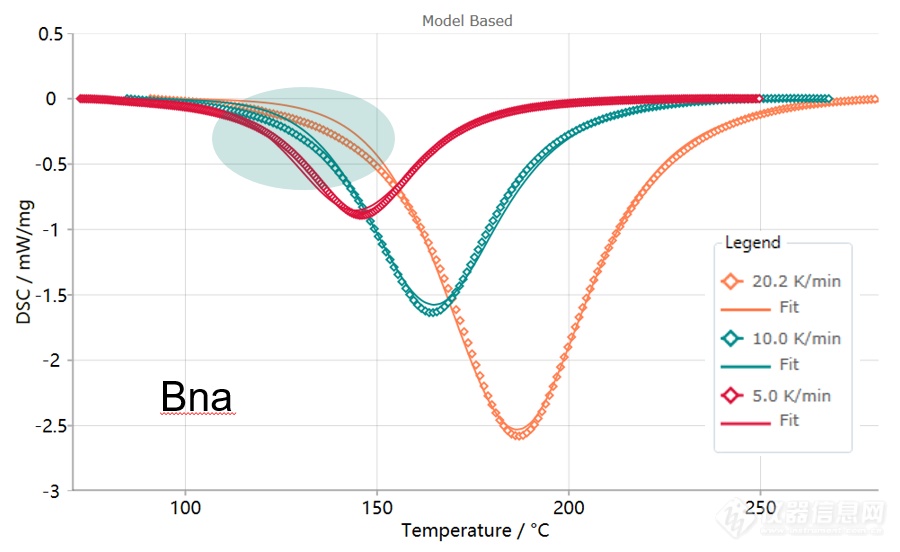
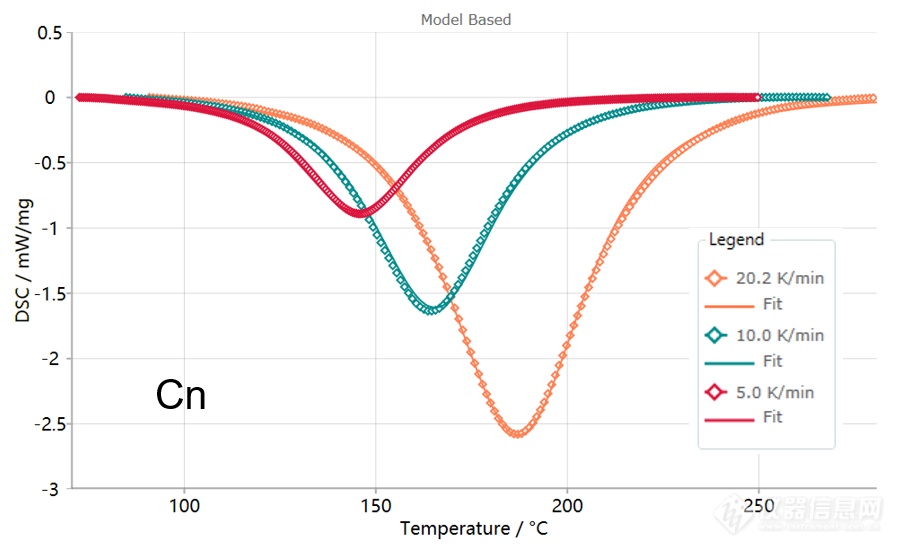
  下图是用复合式自催化函数Cn得到的拟合结果。此处实测线与拟合线几乎完美吻合，表明反应机理可能为级数路径与自催化路径的组合：

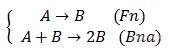
  热分析动力学是化学动力学与热分析实验手段相结合的一门分支学科，它将影响反应速率的各类因素进行筛选、提炼与抽象，简化为温度与转化率的函数，应用于实验数据的归纳，与不同控温程序下实验结果的预测，或按照速率控制要求对控温程序进行优化。

  反应体系可大致分为均相体系与异相体系。均相体系中较为常见的反应机理有级数反应与自催化反应。除温度影响之外，级数反应的速率变化仅与反应物的消耗相关，自催化反应则额外引入了产物生成对反应的加速效应。

  不同的反应类型，在动力学上使用不相同的机理函数进行表征，在热分析曲线上则有不一样的规律性表现(诱导期-加速-减速特性)。在对反应本身的化学机制缺乏了解的情况下，我们大家可以通过对实测热分析曲线选不一样的机理函数进行拟合对比，根据拟合效果、与动力学参数结果的合理性，来猜测可能的反应机理。

  超短链全氟烷基化合物“三氟乙酸”分析利器——超临界流体色谱质谱联用技术

  1240万！新疆医科大学新疆医科大学中心、成都市成华区疾病预防控制中心和河池市疾病预防控制中心检验测试仪器、耗材采购项目

  创新引领 YOUNG帆起航——仪器信息网25周年 我们不一YOUNG！

  北京市理化分析测试中心关于开展“闪光法测定高温合金热扩散系数”实验室间比对的通知